Jose Mathew is an Assistant Professor at The Cochin College since 2019 June. Previously he was doing his PhD at IISERTVM, where he have also served as a teaching assistant.
Teaching Experience
Teaching Approach
He encourage students to explore new areas and to take up challenges. He tries to foster love and passion towards the subject. He prioritize giving open book exams, projects, and assignments to cultivate critical thinking.
Tutorship
Courses handling in 2025-2025 Odd Semester
Select a course to view the detailed syllabus and notes:
For Competitive Exams
Courses handling in 2024-2025 Even Semester
Select a course to view the detailed syllabus and notes:
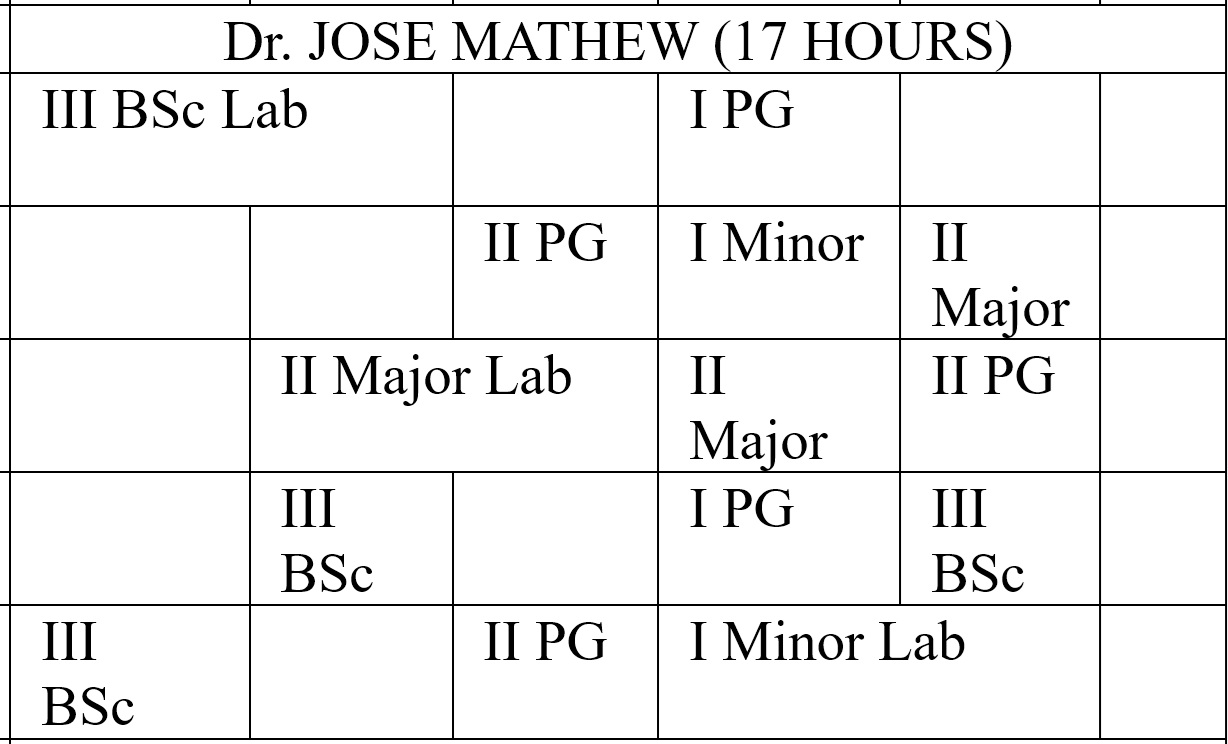
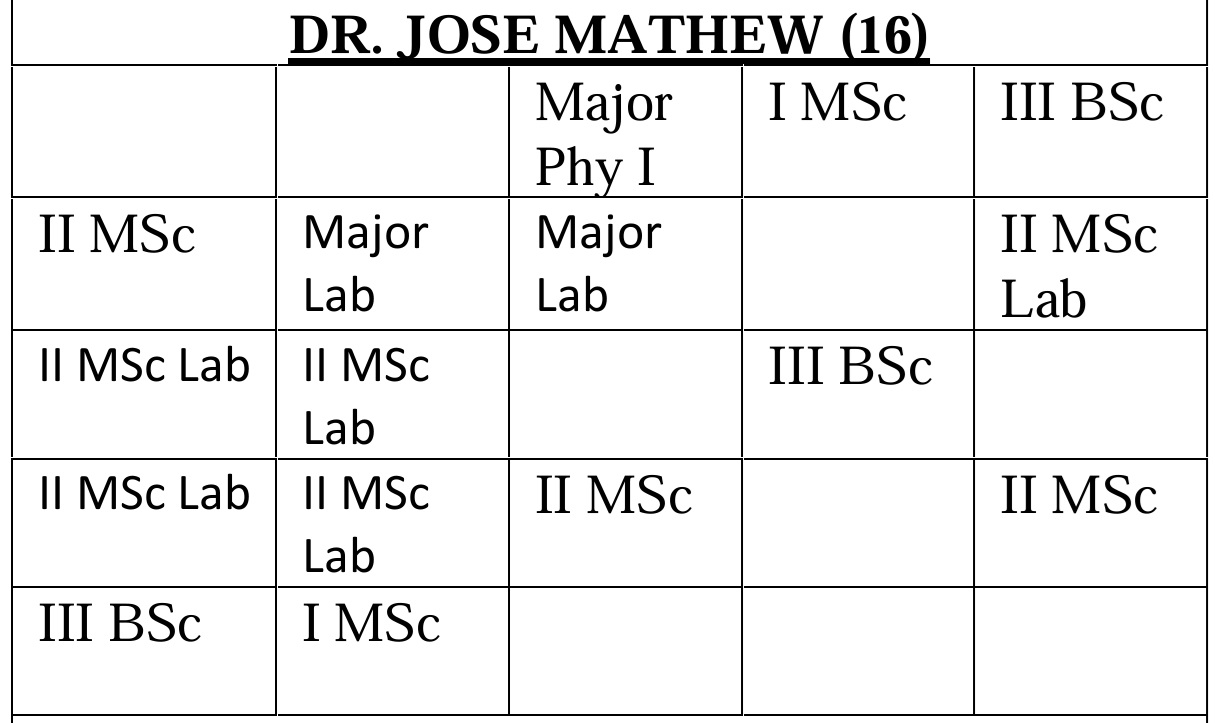
Time Table
Courses handled in 2024-2025 Odd Semester
Select a course to view the detailed syllabus and notes:
In my career spanning last five years, I have taught a variety of courses at The cochin college, including:
Courses handled in the past
Undergraduate Courses
Unit-1 of Thermodynamics and Statistical Physics (Sem 5)
Cosmology
Wave optics
Oscillations and Waves
Properties of Matter
Postgraduate Courses
Classical Mechanics
Unit I and Unit II (2019-2020)
Unit I, Unit III and Unit IV (2020-2023).
Unit III and Unit IV (2023-2024)
UNIT 1
Lagrangian formulation (14 hrs)
1.1 Review of Newtonian Mechanics: Mechanics of a Particle; Mechanics of a System of Particles; Constraints; 1.2 D' Alembert's principle and Lagrange’s equations; velocity-Dependent potentials and the Dissipation Function; Lagrangian for a charged particle in electromagnetic field; 1.3 Application of Lagrange’s equation to: motion of a single particle in Cartesian coordinate system and plane polar coordinate system; bead sliding on a rotating wire.1.4 Hamilton’s Principle; Technique of Calculus of variations; The Brachistochrone problem. 1.5 Derivation of Lagrange’s equations from Hamilton’s Principle. 1.6 Canonical momentum; cyclic coordinates; Conservation laws and Symmetry properties- homogeneity of space and conservation of linear momentum; isotropy of space and conservation of angular momentum; homogeneity of time and conservation of energy; Noether’s theorem(statement only; no proof is expected).
Hamiltonian formulation: (4hrs)
1.7 Legendre Transformations; Hamilton’s canonical equations of motion; Hamiltonian for a charged particle in electromagnetic field. 1.8 Cyclic coordinates and conservation theorems; Hamilton’s equations of motion from modified Hamilton’s principle
UNIT II
Small oscillations (8hrs)
2.1 Stable equilibrium unstable equilibrium and neutral equilibrium; motion of a system near stable equilibrium-Lagrangian of the system and equations of motion. 2.2 Small oscillations- frequencies of free vibrations; normal coordinates and normal modes 2.3 system of two coupled pendula-resonant frequencies normal modes and normal coordinates ;free vibrations of CO2 molecule- resonant frequencies normal modes and normal coordinates.
Canonical transformations and poisson brackets (10 hrs)
2.4 Equations of canonical transformations; Four basic types of generating functions and the corresponding basic canonical transformations. Examples of canonical transformations - identity transformation and point transformation. 2.5 Solution of harmonic oscillator using canonical transformations. 2. 6 Poisson Brackets ; Fundamental Poisson Brackets; Properties of Poisson Brackets 2.7 Equations of motion in Poisson Bracket form; Poisson Bracket and integrals of motion; Poisson’s theorem; Canonical invariance of the Poisson bracket.
UNIT III
Central force problem (9hours)
3.1 Reduction of two-body problem to one-body problem; Equation of motion for conservative central forces - angular momentum and energy as first integrals; law of equal areas 3.2 Equivalent one-dimensional problem –centrifugal potential; classification of orbits. 3.3 Differential Equations for the orbit; equation of the orbit using the energy method; The Kepler Problem of the inverse square law force; S cattering in a central force field - Scattering in a Coulomb field and Rutherford scattering cross section.
Rigid body dynamics (9hrs)
3.4 Independent coordinates of a rigid body; Orthogonal transformations ; Euler Angles. 3.5 Infinitesimal rotations: polar and axial vectors; rate of change of vectors in space and body frames; Coriolis effect. 3.6 Angular momentum and kinetic energy of motion about a point; Inertia tensor and the Moment of Inertia; Eigenvalues of the inertia tensor and the Principal axis transformation . 3.7 Euler equationsof motion; force free motion of a symmetrical top.
UNIT IV
Hamilton-Jacobi theory and action-angle variables(12 hrs)
4.1 Hamilton-Jacobi Equation for Hamilton’s Principal Function; physical significance of the principal function. 4.2 Harmonic oscillator problem using the Hamilton-Jacobi method. Hamilton-Jacobi Equation for Hamilton’s characteristic function 4.3 Separation of variables in the Hamilton-Jacobi Equation; Separability of a cyclic coordinate in Hamilton-Jacobi equation; Hamilton-Jacobi equation for a particle moving in a central force field(plane polar coordinates) . 4.4 Action-Angle variables; harmonic oscillator problem in action-angle variables.
Classical mechanics of relativity ( 6 hrs.)
4.5 Lorentz transformation in matrix form; velocity addition; Thomas precession. 4.6 Lagrangian formulation of relativistic mechanics; Application of relativistic Lagrangian to (i)motion under a constant force (ii) harmonic oscillator and (iii) charged particle under constant magnetic field.
Statistical Mechanics
Unit I, Unit II and Unit III on a slot of 3 X 18 hrs (2019-2023).
Sections 1.2 (unit I) to 2.1.5 (unit II) on a slot of 1 X 18 hrs (2023-2024)
UNIT I (22 hrs)
1.1. The Statistical Basis of Thermodynamics1.1.1. Macroscopic and microscopic states.1.1.2.Connection between thermodynamics and statistics.1.1.3.Classical ideal gas.1.1.4.Entropy of mixing and Gibbs paradox.1.1.5. Correct enumeration of micro states.1.2. Elements of Ensemble Theory 1.2.1. Phase space of a classical system. 1.2.2. Liouville’s theorem.1.2.3. Micro-canonical ensemble.1.2.4. Quantum states and phase space.1.3. Canonical ensemble.1.3.1. Equilibrium between a system and a heat reservoir.1.3.2. System in canonical ensemble.1.3.3. Physical significance of statistical quantities in canonical ensemble.1.3.4. Classical systems.1.3.5. Energy fluctuations in canonical ensemble.1.3.6.Equipartition theorem.
UNIT II (18 hrs)
2.1. Grand canonical Ensemble2.1.1. Equilibrium between system and energy-particle reservoir.2.1.2.A system in grand canonical ensemble.2.1.3.Physical significance of various statistical quantities.2.1.4. Examples.2.1.5. Fluctuations in grand canonical ensemble.2.2. Formulation of Quantum Statistics2.2.1.Quantum mechanical ensemble theory.2.2.2.Density matrix.2.2.3.Statistics of various ensembles.2.2.4.Examples (an electron in magnetic feilds, free particle in a box). 2.2.5. A system composed of indistinguishable particles.
UNIT III(22hrs)
3.1. Quantum Theory of Simple Gases3.1.1. Ideal gas in quantum-micro canonical ensemble.3.1.2.Ideal gas in other quantum mechanical ensembles.3.1.3.Statistics of the occupation numbers3.2.Ideal Bose Systems3.2.1.Thermodynamic behaviour of ideal Bose gas.3.2.2.Thermodynamics of black body radiation. The field of sound waves .3.3. Ideal Fermi Systems3.3.1.Thermodynamics of ideal Fermi gas.3.3.2.Magnetic behaviour of ideal fermi gas.3.3.3.Electron gas in metals.4.
Quantum Mechanics II
Unit IV (2019-2024)
UNIT IV
Relativistic Quantum Mechanics(18 hrs)
4.1 Klein-Gordon Equation; continuity equation and probability density in Klein Gordon theory. 4.2 Non-relativistic limit of the Klein-Gordon equation 4.3 Solutions of the Klein –Gordon equation for positive, negative and neutral spin0 particles; Klein-Gordon equation in the Schrodinger form. 4.4 Dirac Equation in the Scrodinger form; Dirac’s matrices and their properties 4.5 Solutions of the free particle Dirac equation; single particle interpretation of the plane waves; velocity operator; zitterbewegung4.6 Non-relativistic limit of the Dirac equation; spin of Dirac particles; Total angular momentum as a constant of motion. 4.7 Negative energy states and Dirac’s hole theory.
Along with these I have taken parts of other courses like
Perturbation theory of QM-II
Mathematical Methods-I (vector spaces, curvilinear coordinates, Probability theory and distribution)
Atomic Spectra, and Raman Spectroscopy and Electronic Spectroscopy, of Atomic and Molecular Spectra
Parts of NANOSTRUCTURES AND MATERIALS CHARACTERISATION
Mentoring
Additionally, I have mentored several graduate and post graduate projects, including:
Undergraduate Student Projects
- Bricks (A computer graphics game in C++, implementing Newtonian gravity and Numerical integration)
- Modelling Diffusion using Random Walk
- Lagrange Points
- Deriving Friedmann equations
Postgraduate Student Projects
- A review of- Big-bang, Problems of Big-bang and Possible Solutions. And, a new model of bounce (Miss. Krishnendu Hareendran (190011020252) Miss ANJU LAL (190011020247) Miss. SANDHRA KAMALAHASAN (190011020254))
- FLRW Cosmology and the Friedmann Equations (Kevin Chacko Mundackal)
- Stability Analysis of Power Law Inflation (Rijo Raju)